Your Work done by electric field equation images are available. Work done by electric field equation are a topic that is being searched for and liked by netizens today. You can Download the Work done by electric field equation files here. Download all free photos and vectors.
If you’re looking for work done by electric field equation pictures information related to the work done by electric field equation keyword, you have visit the ideal blog. Our website always gives you suggestions for seeing the maximum quality video and image content, please kindly hunt and find more informative video articles and images that fit your interests.
Work Done By Electric Field Equation. Thus the work done on the charged particle by the electric field as the particle moves from point P 1 to P. W T Δ θ where Δ θ is the angle of rotation. Shows you how to calculate the work done by an electric field when it moves a charge through a potential difference. W q E d If the charge is positive and the charge moves in the direction of the electric field to by convention solely under the influence of the field the field does positive work on the charge.
Electric Fields And Potentials Physics A Level From physbot.co.uk
Clearly the work done ie energy lost by the field equals the decrease in potential energy of the charge Thus The total energy of the electron is made up of two components–the electric potential energy and the kinetic energy. Dr Here electrostatic force Fq Eqyixj F. The work per unit charge done by the electric field along an infinitesmal path length ds is given by the scalar product. WE_pA - E_pB The electric field potential is equal to the potential energy of a charge equal to 1 C. We want the rest particle to move with a constant velocity So. Therefore the work done by the electric field here will be.
But keep in mind that it is only the differences in electric potential that have any meaning.
WUqVqVV qV rr where the last step is done by our convention. Therefore the work done by the electric field here will be. An electric field is given by EyixNC 1. The work per unit charge done by the electric field along an infinitesmal path length ds is given by the scalar product. WE_pA - E_pB The electric field potential is equal to the potential energy of a charge equal to 1 C. When two metallic plates are set a.
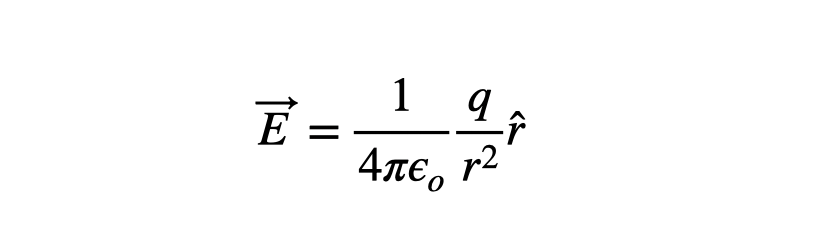Source: medium.com
It accelerates the charge gaining kinetic energy equal to the work done by the field. Lets call the charge that you are trying to move Q. WUqVqVV qV rr where the last step is done by our convention. Clearly the work done ie energy lost by the field equals the decrease in potential energy of the charge Thus The total energy of the electron is made up of two components–the electric potential energy and the kinetic energy. It accelerates the charge gaining kinetic energy equal to the work done by the field.
Source: bilimfili.com
We know that the work done by an electric field is W q V Here W Work done q The magnitude of the charge V V A V B The difference in the electric potential between the two points So W 005 200 100 5 J. A constant offset in electric potential or potential energy does not affect anything. Lets call the charge that you are trying to move Q. What is the equation of the work done by the electric field on the electron. But keep in mind that it is only the differences in electric potential that have any meaning.
Source: physics.stackexchange.com
A constant offset in electric potential or potential energy does not affect anything. W T Δ θ where Δ θ is the angle of rotation. Lets call the charge that you are trying to move Q. The work done by the electric field in moving an electric charge from infinity to point r is given by. Work - It is the work done in moving a charge q from infinity to a distance r in the electric field.
Source: youtube.com
The magnitude of the force is the charge of the particle times the magnitude of the electric field F q E so B53 W 23 q E b. A constant offset in electric potential or potential energy does not affect anything. Work - It is the work done in moving a charge q from infinity to a distance r in the electric field. Combining these two equations with the fact that the convention defining electric field vector shows you the direction of the Force acting on a unit ve test charge will surely help u solve the problem. Lets call the charge that you are trying to move Q.
Source: slideplayer.com
The work per unit charge done by the electric field along an infinitesmal path length ds is given by the scalar product. We want the rest particle to move with a constant velocity So. WUqVqVV qV rr where the last step is done by our convention. Then the work done against the field per unit charge in moving from A to B is. When two metallic plates are set a.
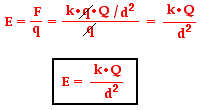Source: physicsclassroom.com
It accelerates the charge gaining kinetic energy equal to the work done by the field. Combining these two equations with the fact that the convention defining electric field vector shows you the direction of the Force acting on a unit ve test charge will surely help u solve the problem. W q E d If the charge is positive and the charge moves in the direction of the electric field to by convention solely under the influence of the field the field does positive work on the charge. An electric field is given by EyixNC 1. The work per unit charge done by the electric field along an infinitesmal path length ds is given by the scalar product.
Source: penguinphysic.wordpress.com
It accelerates the charge gaining kinetic energy equal to the work done by the field. When two metallic plates are set a. WUqVqVV qV rr where the last step is done by our convention. We want the rest particle to move with a constant velocity So. W where is the force that is applied against the net force because of the electric field and d is a differential displacement vector along the way from a to b.
Source: physbot.co.uk
The torque experienced by an electric dipole with dipole moment p in an electric field E is T p E p E sin θ were θ is the angle between the dipole moment and the electric field. WUqVqVV qV rr where the last step is done by our convention. Work done by an electric force by transfering a charge in an electric field is equal to the difference of potential energies between the starting position A and the final position B. Clearly the work done ie energy lost by the field equals the decrease in potential energy of the charge Thus The total energy of the electron is made up of two components–the electric potential energy and the kinetic energy. Shows you how to calculate the work done by an electric field when it moves a charge through a potential difference.
Source: sites.science.oregonstate.edu
Find the work done in J by the electric field in moving a 1 C charge from rA 2i2jm to rB 4ij m A 0 J B 2 J C 2 J D 4 J Hard Solution Verified by Toppr Correct option is A 0 J Work done W F. The change in voltage is defined as the work done per unit charge so it can be in general calculated from the electric field by calculating the work done against the electric field. We want the rest particle to move with a constant velocity So. Work done by an electric force by transfering a charge in an electric field is equal to the difference of potential energies between the starting position A and the final position B. W T Δ θ where Δ θ is the angle of rotation.
Source: physicsclassroom.com
Then the work done against the field per unit charge in moving from A to B is. And the work done by an electric field is always equal to. WUqVqVV qV rr where the last step is done by our convention. The torque experienced by an electric dipole with dipole moment p in an electric field E is T p E p E sin θ were θ is the angle between the dipole moment and the electric field. Observe that if you want to calculate the work done by the electric field on this charge you simply invoke W e l e c t r i c f i e l d Q R 1 R 2 E d r this follows immediately from definition of electric force.
Source: slideplayer.com
What is the equation of the work done by the electric field on the electron. The magnitude of the force is the charge of the particle times the magnitude of the electric field F q E so B53 W 23 q E b. Thus the work done on the charged particle by the electric field as the particle moves from point P 1 to P. But keep in mind that it is only the differences in electric potential that have any meaning. It accelerates the charge gaining kinetic energy equal to the work done by the field.
Source: quora.com
Work - It is the work done in moving a charge q from infinity to a distance r in the electric field. Clearly the work done ie energy lost by the field equals the decrease in potential energy of the charge Thus The total energy of the electron is made up of two components–the electric potential energy and the kinetic energy. It accelerates the charge gaining kinetic energy equal to the work done by the field. What is the equation of the work done by the electric field on the electron. We know that the work done by an electric field is W q V Here W Work done q The magnitude of the charge V V A V B The difference in the electric potential between the two points So W 005 200 100 5 J.
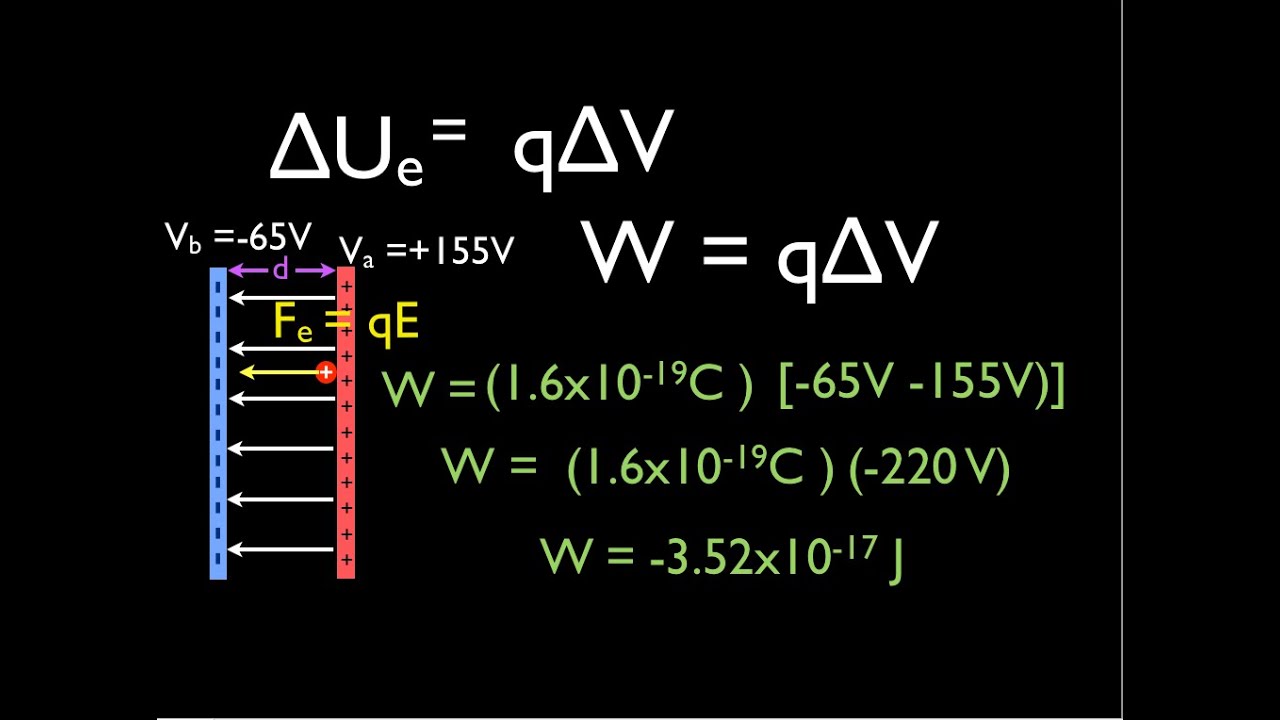Source: youtube.com
An electric field is given by EyixNC 1. WUqVqVV qV rr where the last step is done by our convention. It accelerates the charge gaining kinetic energy equal to the work done by the field. Combining these two equations with the fact that the convention defining electric field vector shows you the direction of the Force acting on a unit ve test charge will surely help u solve the problem. The change in voltage is defined as the work done per unit charge so it can be in general calculated from the electric field by calculating the work done against the electric field.
Source: physbot.co.uk
We want the rest particle to move with a constant velocity So. Therefore the work done by the electric field here will be. WE_pA - E_pB The electric field potential is equal to the potential energy of a charge equal to 1 C. Shows you how to calculate the work done by an electric field when it moves a charge through a potential difference. W where is the force that is applied against the net force because of the electric field and d is a differential displacement vector along the way from a to b.
Source: study.com
The work per unit charge done by the electric field along an infinitesmal path length ds is given by the scalar product. We want the rest particle to move with a constant velocity So. Find the work done in J by the electric field in moving a 1 C charge from rA 2i2jm to rB 4ij m A 0 J B 2 J C 2 J D 4 J Hard Solution Verified by Toppr Correct option is A 0 J Work done W F. What is the equation of the work done by the electric field on the electron. But keep in mind that it is only the differences in electric potential that have any meaning.
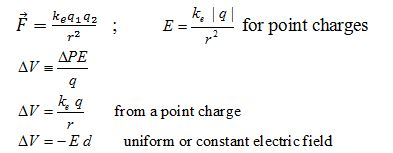Source: chegg.com
Shows you how to calculate the work done by an electric field when it moves a charge through a potential difference. Work - It is the work done in moving a charge q from infinity to a distance r in the electric field. WUqVqVV qV rr where the last step is done by our convention. We know that the work done by an electric field is W q V Here W Work done q The magnitude of the charge V V A V B The difference in the electric potential between the two points So W 005 200 100 5 J. But keep in mind that it is only the differences in electric potential that have any meaning.
Source: quora.com
And the work done by an electric field is always equal to. When two metallic plates are set a. Combining these two equations with the fact that the convention defining electric field vector shows you the direction of the Force acting on a unit ve test charge will surely help u solve the problem. W q E d If the charge is positive and the charge moves in the direction of the electric field to by convention solely under the influence of the field the field does positive work on the charge. Work - It is the work done in moving a charge q from infinity to a distance r in the electric field.
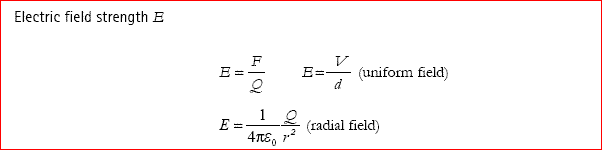Source: cyberphysics.co.uk
The change in voltage is defined as the work done per unit charge so it can be in general calculated from the electric field by calculating the work done against the electric field. WUqVqVV qV rr where the last step is done by our convention. An electric field is given by EyixNC 1. Dr Here electrostatic force Fq Eqyixj F. The change in voltage is defined as the work done per unit charge so it can be in general calculated from the electric field by calculating the work done against the electric field.
This site is an open community for users to share their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site good, please support us by sharing this posts to your own social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title work done by electric field equation by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
